Veke 3–4. Eksponentialfunksjonen
Eksponentialfunksjonen
3.1 Eksponentialfunksjonen
Eksempeloppgåve 3.1 (Sparekonto) Ola har ein sparekonto med 3% rente. Han set inn 1000 kr. ved starten av året. Kva er saldoen etter ...
- 1.
- 100 år?
- 2.
- år?
Løysing 3.1 Me ser av oppgåve 3.1, at me gongar med vekstfaktoren ein gong for kvart år som går. Saldoen etter eitt år er
Etter to år er han
Etter tre år er han
Dette mynsteret held fram slik at me kan skriva saldoen etter år som
Etter 100 år har me , og kan skriva
Merk at dette òg gjeld etter null år (), fordi
Øvingsoppgåve 3.2 Kari har ein sparekonto med rente. Ho set inn 2000 kr. Kva er saldoen etter 50 år?
Øvingsoppgåve 3.3 () Bente låner kr. til ferie, med % rente per år. Ho skal betala tilbake heile lånet om fem år, med renter. (Rentene vert lagt til lånet ved utgangen av kvart år.) Kor mykje må ho betala?
Eksempeloppgåve 3.4 Tenk deg at du set inn 100 kr. i banken til 10% rente. Saldoen etter år er gjeven ved funksjonen . Korleis utvikler saldoen seg over lang tid? Plott funksjonen som ei kurve. (Du kan velja om du vil teikna for hand eller bruka datamaskin eller kalkulator.)
Løysing 3.2 Det er greitt å plotta for hand. Me reknar ut eit par verdiar for med kalkulator, plottar punktane etter beste skjønn, og teiknar kurva på frihand. Dette er nøyaktig nok til å sjå korleis eksponentialfunksjon veks raskare og raskare når aukar.
| 0 | 100 |
| 10 | 259,3742 |
| 20 | 672,7500 |
| 30 | 1744,9402 |
| 50 | 11 739,0853 |
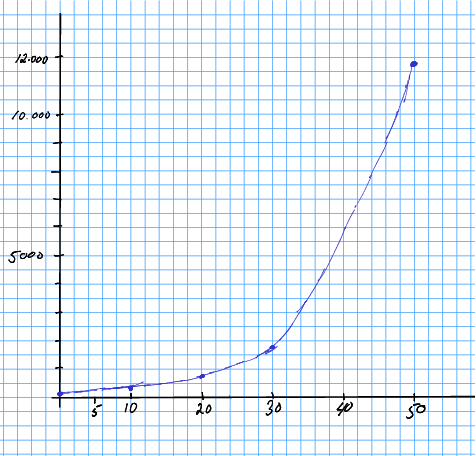
Merknad 3.1 Dersom du vil plotta på maskin, og ikkje har egna programvare installert, so kan Wolfram Alpha vera eit godt alternativ. For å løysa oppgåva over i Wolfram Alpha, skriv:
plot 100*1.1^t for t=0...50
Elles kan du like gjerne bruka programvare eller kalkulator som du kjenner frå før.
Øvingsoppgåve 3.5 Tenk deg at du set 1000 kr. i aksjefond og får 25% avkasting. Verdien av innskotet etter år er gjeve ved funksjonen . Plott verdiutviklinga som ei kurve. (Du kan velja om du vil teikna for hand eller bruka datamaskin eller kalkulator.)
Definisjon 3.1 Ein funksjon på formen vert kalla ein eksponentialfunksjon.
Øvingsoppgåve 3.6 Lag eit plot for å samanlikna verdiutviklinga med 1%, 5% og 10% rente. Lat startverdien vera 1000 kroner.
Øvingsoppgåve 3.7 Lag eit plot som samanliknar funksjonane og for .
Øvingsoppgåve 3.8 Bruk plottet i forrige oppgåve til å finna omtrentleg -verdi slik at .