Veke 12. Den andrederiverte
Krumming
13.2 Krumming
Eksempeloppgåve 13.5 Ein funksjon er gjeven som fylgjande kurve:
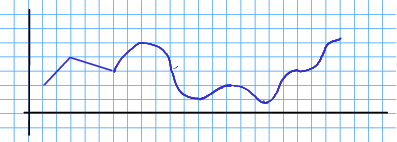
Skissér og basert på kurva over.
Løysing 13.3 Me skisserer basert på slik at får positiv verdi når fell og negativ når stig. Me skisserer på same måte basert på .
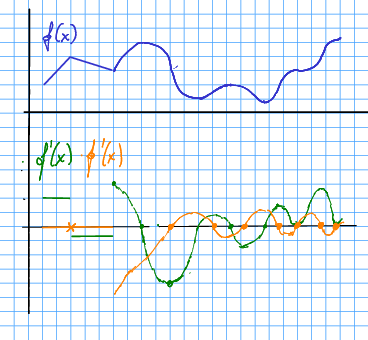
Merk at skissa ikkje er perfekt, men me kan sjå nokonlunde kvar og har null-, topp- og botnpunkt. Me kan òg sjå kvar dei er konstante. Legg merke til -ane, som viser punkt der er udefinert.
Øvingsoppgåve 13.6 Ein funksjon er gjeven som fylgjande kurve:
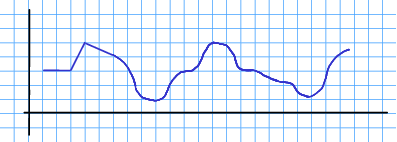
Skissér og basert på kurva over.
Eksempeloppgåve 13.7 Ein funksjon er gjeven som fylgjande kurve:
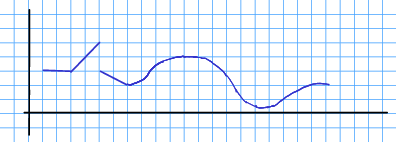
Skissér basert på kurva over.
Løysing 13.4 Me skisserer basert på slik at er positiv når krummar oppover og negativ når krummar nedover.
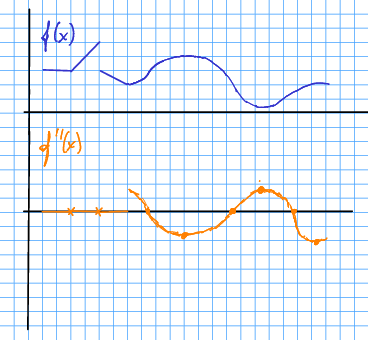
Merk at skissa ikkje er perfekt, men me kan sjå nokonlunde kvar har null-, topp- og botnpunkt. Me kan òg sjå kvar dei er konstante. Legg merke til -ane, som viser punkt der er udefinert.
Øvingsoppgåve 13.8 Ein funksjon er gjeven som fylgjande kurve:
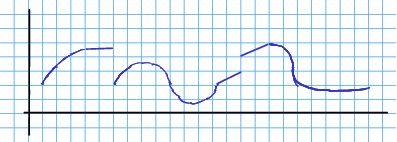
Skissér basert på kurva over.