Veke 7. Lineær kostnad og inntekt

Eksempeloppgåve 8.8 Lat oss studera økonomien i det lokale bryggeriet. Prisen dei får frå serveringsstadene er 22 kroner per liter øl, som gjev inntektsfunksjonen $I\left(x\right)=22x$. Dei har 10 000 kroner i faste kostnader, og 7 kroner per liter i variable kostader. Dvs. at kostnadsfunksjonen er $K\left(x\right)=10000+7x$.

1.

Plott $K\left(s\right)$ og $I\left(x\right)$ i same koordinatsystem.

2.

Basert på plottet, omtrent kor mange liter øl må bryggeriet selja for å gå i balanse.

Løysing 8.4

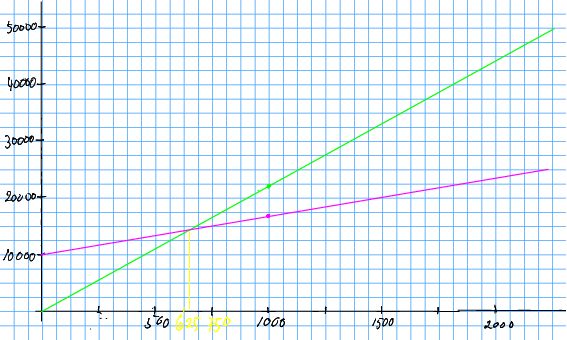
Der linene kryssar, er inntekta like stor som kostnaden, og bryggeriet går i balanse. Me ser ikkje eksakt på literen kvar det skjer, men me ser at det skjer i ruta mellom 625 liter og 677$\frac{1}{2}$ liter. Lat oss seia cirka 650 liter.

Merknad 8.2 I oppgåve 8.11 skal me sjå at eksakt svar er $666\frac{2}{3}$ liter, men so nøyaktig klarer me ikkje å sjå på eit handteikna plott på so grovt rutenett.

Øvingsoppgåve 8.9 Sandtaket på Mo sel sand for 600 kr tonnet, slik at dei har inntektsfunksjonen $I\left(x\right)=600\cdot x$. Kostnaden for å produsera eit tonn sand er 300 kr, i tillegg til faste kostnader på 100 000 kr. Dvs. at kostnadsfunksjonen er $K\left(x\right)=\text{100 000}+300x$.

1.

Plott $K\left(s\right)$ og $I\left(x\right)$ i same koordinatsystem.

2.

Basert på plottet, omtrent kor mange tonn sand må sandtaket selja for å gå i balanse?

Øvingsoppgåve 8.10 Lasses bensinstasjon sel bensinen for 16 kr literen. Bensinen kostar 8 kr i innkjøp. I tillegg kostar det 32 000 kr å halda bensinstasjonen i drift.

1.

Sett opp ein inntektsfunksjon $I\left(x\right)$ for Lasse.

2.

Sett opp ein kostnadsfunksjon $K\left(x\right)$ for Lasse.

3.

Plott $K\left(s\right)$ og $I\left(x\right)$ i same koordinatsystem.

4.

Basert på plottet, omtrent kor mange liter bensin må Lasse selja for å gå i balanse?

Eksempeloppgåve 8.11 Lat oss gå tilbake til bryggeriet i oppgåve 8.8. Finn eksakt produksjonsvolum $x$ som gjev balanse mellom inntektene gjeve som $I\left(x\right)=22x$ og kostnadene gjeve som $K\left(x\right)=10000+7x$.

Løysing 8.5 Balanse vil seia at kostnadene er lik inntektene, mao.

$$\begin{array}{lll}\hfill I\left(x\right)& =K\left(x\right),& \hfill \text{(56) }\\ \hfill 22x& =10000+7x.& \hfill \text{(57) }\end{array}$$

Dei to sidene i likninga er like. Om me gjer same operasjon på båe sider, er dei stadig like. Målet no er å bli kvitt $x$-en på den eine sida, so me trekk frå $7x$; slik:

$$\begin{array}{lll}\hfill 22x-7x& =10000+7x-7x,& \hfill \text{(58) }\\ \hfill 15x& =10000.& \hfill \text{(59) }\end{array}$$

No har me eit uttrykk for $15x$, men me vil ha eit uttrykk for ein $x$. Då må må me dela på $15$, slik:

$$\begin{array}{lll}\hfill x& =\frac{10000}{15}=\text{666,67}.& \hfill \text{(60) }\end{array}$$

Bryggeriet må altso produsera 666,67 liter øl for å gå i balanse.

Øvingsoppgåve 8.12 Lat oss sjå igjen på Sandtaket på Mo frå oppgåve 8.9. Inntektsfunksjonen er $I\left(x\right)=600\cdot x$ og kostnadsfunksjonen $K\left(x\right)=\text{100 000}+300x$. Finn produksjonsvolument $x$ som gjev balanse i drifta.

Øvingsoppgåve 8.13 Gå tilbake til Lasses bensinstasjon i oppgåve 8.10. Bruk inntektsfunksjonen og kostnadsfunksjonen som du fann, og finn ut kor mykje bensin Lasse må selja får å gå i balanse.

Eksempeloppgåve 8.14 Hilde går på sirkus saman med to nevøar. Hilde betaler vaksenbillett, medan nevøane får barnebillett. Barnebilletten kostar to tredjedelar av vaksenbilletten. Til saman betaler dei 420 kroner. Kor mykje kostar vaksenbilletten?

Løysing 8.6 Her må me setja opp ein modell over billettprisane. Dette kan gjerast på litt ulike måtar, avhengig av kor mykje ein gjer i hodet og kva ein helst vil ha skrive ned.

Lat $x$ vera prisen på vaksenbilletten. Det er talet som me vert spurde om. Me kan la prisen på barnebilletten vera $y$. Totalprisen kan me då skriva som $x+2y$ kroner. Me har òg fått vita at totalprisen er 420 kroner. Dette gjev ei likning:

Likninga har to ukjende, men ho er lett å forenkla. Oppgåva seier at barnebilletten er to tredjedelar av vaksenbilletten. Matematisk kan me skriva

No kan me byta ut prisen $y$ i den fyrste likninga:

og då har likninga berre éin ukjend. Me kan verta kvitt brøken ved å gonga gjennom med nemnaren:

eller

Ein $x$ er ein sjuandedel av $7x$, so me kan skriva

Vaksenbilletten kostar altso 180 kroner.

Øvingsoppgåve 8.15 Mor, far og tre born tek bussen. Dei betaler 140 kroner totalt. Barnebilletten kostar halvparten av vaksenbilletten. Kor mykje kostar ein vaksenbillett?

Øvingsoppgåve 8.16 Harry kjøper to liter mjølk og åtte liter øl. Mjølka kostar 18 kroner literen og han betaler 630 kroner totalt. Kor mykje kostar ølet per liter?

Øvingsoppgåve 8.17 Line blandar saft i forholdet 1:4, dvs. fire gongar so mykje vatn som saft. Ho får åtte desiliter ferdig saft. Kor mykje konsentrert saft har ho brukt?