Veke 7. Lineær kostnad og inntekt

Øvingsoppgåve 8.1 Piddien sel strikkevantar. Han tener 100 kroner på kvart par han sel. Kor mykje tener han når han sel ti par?

Eksempeloppgåve 8.2 Ålesund Dings og Profitt AS sel dingsar. Dei har rekna på kostnadene ved ulike produksjonsvolum, og kome fram til fylgjande. Produksjon av 100 dingsar: kr. 2000; 200 dingsar: kr. 3000; 400 dingsar: kr. 5000; 600 dingsar: kr. 6500. Visualiser samanhengen mellom produksjonsvolum og kostnad i eit plott.

Løysing 8.1

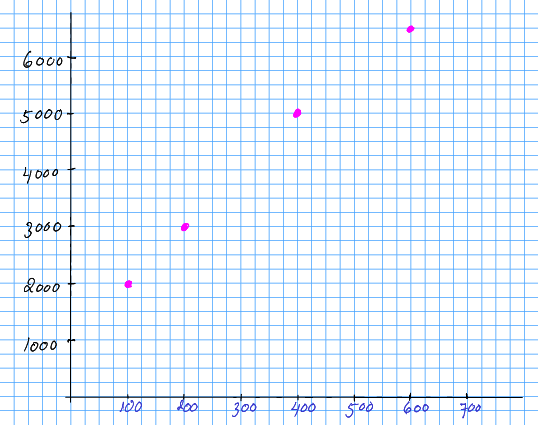
Øvingsoppgåve 8.3 (fortsetjing av forrige oppgåve) Ålesund Dings og Profitt AS har rekna ut ytterlegare eit par kostnadsdøme. Produksjon av 300 dingsar: kr. 4000 og produksjon av 700 dingsar: kr. 6400. Legg til desse to datapunkta i løysinga frå forrige oppgåve.

Eksempeloppgåve 8.4 Piddien sel strikkevantar. Han tener 100 kroner på kvart par han sel. Kor mykje tener han når han sel $x$ par vantar?

1.

Skriv ned ein funksjon som gjev inntekten for $x$ par solgte vantar.

2.

Illustrer samanhengen mellom $x$ og samanlagd inntekt grafisk.

Løysing 8.2 Piddien tener 100 kroner per par. Når han sel $x$ par, tener han $100\cdot x$. kroner Som ein funksjon kan me skriva

der $I\left(x\right)$ er inntekta gjeve at han sel $x$ par.

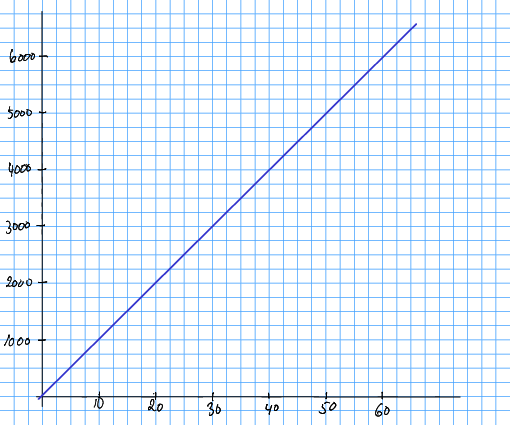
Øvingsoppgåve 8.5 Ålesund Dings og Profitt AS sel dingsar. Utsalsprisen er 25 kroner per dings.

1.

Skriv ned ein funksjon som gjev bruttoinntekta (dvs. før utgiftene er trekt frå) når dei sel $x$ dingsar.

2.

Illustrer samanhengen mellom $x$ og inntekta grafisk.

Eksempeloppgåve 8.6 Lat oss studera produksjonskostnaden hos Ålesund Dings og Profitt AS. Dei har faste kostnader på 1000 kroner; dvs. 1000 kr. som dei må betala uansett kor mange dingsar dei produserer. I tillegg kostar det 10 kroner for kvar dings som vert produsert.

1.

Skriv ned ein funksjon som gjev kostnadene ved produksjon av $x$ dingsar.

2.

Illustrer samanhengen mellom $x$ og kostnadene grafisk.

Løysing 8.3 Dette er eit modelleringsproblem der modellen er kostnadsfunksjonen som skildrar kostnadene som bedrifta har.

Me har to typar kostnader. Dei betaler 10 kr per dings og produserer $x$ dingsar. Det vert totalt $10x$ kr i variable kostnader. Dei andre kostnadene er faste, eller konstante, på 1000 kr. Dei samla kostnadene er summen av alle typar kostnader, altso $1000+10x$.

Lat oss kalla funksjonen for $K\left(x\right)$, berre for å ha eit namn. Då skriv me

Det er svaret på del 1.

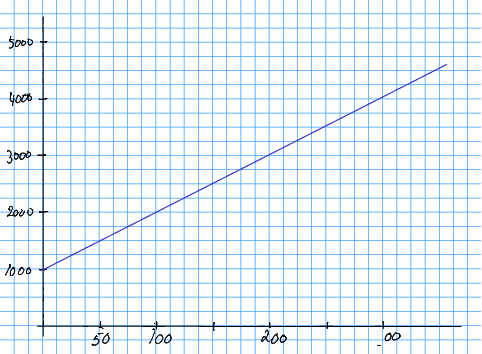
Øvingsoppgåve 8.7 Skreddar Skår lever av å selja handsydde dressar. Han bruker 225 000 kroner i året på faste utgifter til verkstaden (husleige og utstyr). Til kvar dress treng han òg 2000 kroner i materialar. Set opp ein kostnadsfunksjon for skreddaren og plott funksjonen i eit rutenett.

Merknad 8.1 Legg merke til samanhengen mellom ein funksjon og ein graf. Me kan finna det produksjonsvolumet som me ynskjer på $x$-aksen (horisontalaksen), og lesa av kor mykje produksjonen kostar på $y$-aksen (vertikalaksen). Då er det kostnadsfunksjon som me les av.

Me kan òg lesa den inverse funksjonen av det same plottet. Tenk deg at me veit kva me har råd til å betala i produksjonskostnad. Denne kostnaden kan me finna på $y$-aksen, og vha. kurva finn me kva produksjonsvolum me kan makta på $x$-aksen.