Den lineære kostnadsfunksjonen

Eksempeloppgåve 14.3 Ei bedrift har kostnadsfunksjonen

K (x) = 10 x + 50 .

Finn gjennomsnittskostnaden $A (x)$ . Drøft og skisser $A (x)$ og finn kostnadsoptimumet.

Løysing 14.2 Gjennomsnittskostnaden er gjeven som

A (x) = \frac{K (x)}{x} = 10 + \frac{50}{x} .

Lat oss fyrst analysera dei variable og dei faste kostnadene kvar for seg. Me skriv

\begin{align} A_{1} (x) & = 10, & (108) \\ A_{2} (x) & = \frac{50}{x}, & (109) \\ A (x) & = A_{1} (x) + A_{2} (x) . & (110) \end{align}

Legg merke til at $A_{2} (x)$ er udefinert for $x = 0$ , men kva skjer når $x \to 0^{+}$ , dvs. når $x$ er positiv og nærmar seg 0. Når me deler på eit stadig mindre tal, vert brøken stadig større, so $A_{2} (x) \to \infty$ . Omvendt kan me sjå, når $x \to \infty$ , at $A_{2} (x) \to 0^{+}$ .

Me ser òg at $A_{1} (x)$ er konstant, dvs. ei vassrett line, og me kan skissera $A_{1} (x)$ og $A_{2} (x)$ i diagrammet.

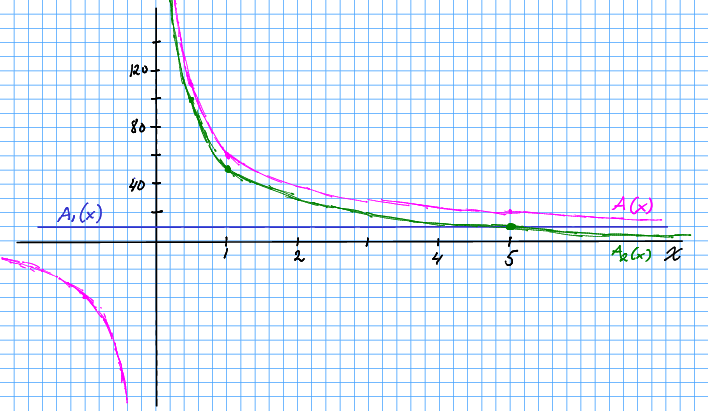
I skissa ser me korleis kurva åt $A_{2} (x)$ nærmar seg $x$ -aksen når $x \to \infty$ , og $y$ -aksen når $A_{2} (x) \to \infty$ . Me har òg skissert $A (x)$ . Sidan $A (x)$ er summen av $A_{2} (x)$ og $A_{1} (x) = 10$ , vert kurva lik $A_{2} (x)$ flytta ti steg opp langs $y$ -aksen.

Me har skissert funksjonen for negative verdiar av $x$ for å illustrera korleis slike funksjonar ser ut generelt. Sidan negativt produksjonsvolum ikkje gjev meining, er dette ikkje relevant for kostnadsfunksjonar.

Kostnadsoptimumet er ikkje definert her. Den lågaste einingskostnaden får me når $x \to \infty$ .

Øvingsoppgåve 14.4 Ei bedrift har kostnadsfunksjonen

K (x) = 2 x + 100 .

Finn gjennomsnittskostnaden $A (x)$ . Kva kan me seia om kostnadsoptimumet?

Veke 13. Kostnadsoptimum

14.2 Den lineære kostnadsfunksjonen