Matematisk Problemløysing 2020

Veke 13. Kostnadsoptimum

Kostnadsoptimum $†$

14.3 Kostnadsoptimum $†$

\begin{align} f (x) & = \frac{1}{x} & (111) \\ f^{'} (x) & = - \frac{1}{x^{2}} & (112) \end{align}

Rekneregel 14.1: Den deriverte av

1 ∕ x

Eksempeloppgåve 14.5 Ei bedrift har kostnadsfunksjonen

K (x) = 0,07 x^{2} - x + 50 .

Finn gjennomsnittskostnaden $A (x)$ . Drøft og skisser $A (x)$ og finn kostnadsoptimumet.

Løysing 14.3 Gjennomsnittskostnaden er gjeven som

A (x) = \frac{K (x)}{x} = 0,07 x - 1 + \frac{50}{x}

Lat oss fyrst analysera dei variable og dei faste kostnadene kvar for seg, slik som me gjorde i oppgåve 14.1. Me skriv

\begin{align} A_{1} (x) & = 0,07 x - 1, & (113) \\ A_{2} (x) & = \frac{50}{x}, & (114) \\ A (x) & = A_{1} (x) + A_{2} (x) . & (115) \end{align}

Gjennomsnittet av dei faste kostnadene, $A_{2} (x)$ , er den same funksjonen som i oppgåve 14.1. Han er udefinert for $x = 0$ , og $A_{2} (x) \to \infty$ når $x \to 0^{+}$ . Når $x \to \infty$ , får me $A_{2} (x) \to 0^{+}$ .

Gjennomsnittet $A_{1} (x)$ av dei variable kostnadene er denne gongen lineært, men ikkje konstant. Me kan skissera $A_{1} (x)$ og $A_{2} (x)$ som fylgjer.

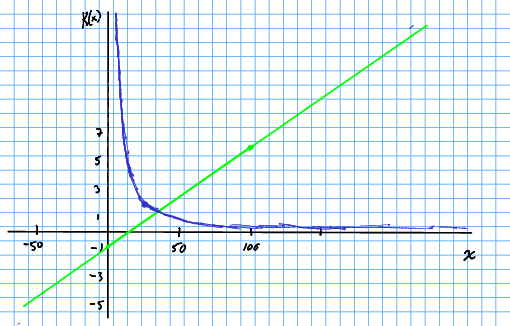
Dersom me legg saman $A_{1} (x)$ og $A_{2} (x)$ skulle me få u nokonlunde fylgjande plott.

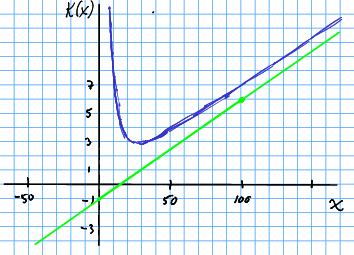
Det ser ut som om me har eit botnpunkt, so lat oss studera det litt nærare ved hjelp av den deriverte. Då treng med rekneregel 14.1. Me kan derivera ledd for ledd, so me har

\begin{align} A (x) & = 0,07 x - 1 + 50 \cdot \frac{1}{x} & (116) \\ A^{'} (x) & = 0,07 + 50 \cdot (- \frac{1}{x^{2}}) = 0,07 - \frac{50}{x^{2}} & (117) \end{align}

Me må løysa likninga

\begin{align} 0 = 0,07 - \frac{50}{x^{2}} . & (118) \end{align}

Dette er ikkje ei vanleg andregradslikning, men me kan gonga gjennom med $x^{2}$ (føresett at $x \neq 0$ ):

\begin{align} 0 \cdot x^{2} & = 0,07 \cdot x^{2} - 50, & (119) \\ 50 & = 0,07 \cdot x^{2} & (120) \\ \frac{50}{0,07} & = x^{2} & (121) \\ x & = \pm \sqrt{\frac{50}{0,07}} \approx \pm 26,73 & (122) \end{align}

Den tilhøyrande $y$ -verdien er

\begin{align} A (26,73) & = 2,74 & (123) \end{align}

Ved hjelp av dette punktet, kan me skissera funksjonen litt meir nøyaktig.

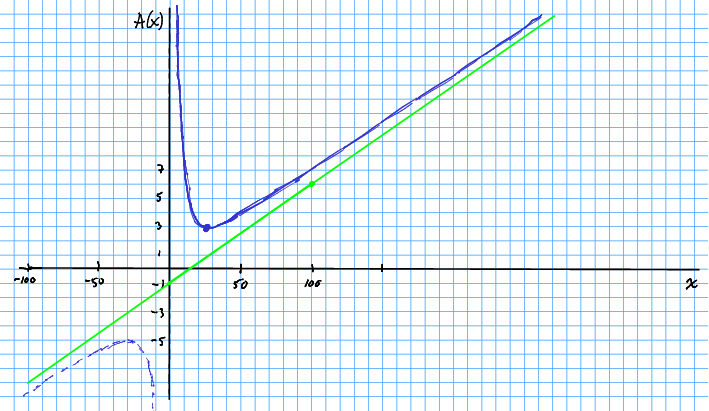
Den lågaste gjennomsnittskostnaden finn me når me produserer $x = 26,73$ einingar.

Øvingsoppgåve 14.6 Ei bedrift har kostnadsfunksjonen

K (x) = 0,05 x^{2} + 2 x + 100 .

Finn gjennomsnittskostnaden $A (x)$ . Drøft og skisser $A (x)$ og finn kostnadsoptimumet.

Merknad 14.2 (Rasjonal funksjon) Funksjonar på formen

f (x) = \frac{p (x)}{q (x)}

der både $p (x)$ og $q (x)$ er polynom, vert kalla rasjonale funksjonar. Når kostnadsfunksjonen $K (x)$ er eit polynom, vert gjennomsnittskostnaden $A (x) = K (x) ∕ x$ ein rasjonal funksjon, sidan $x$ er eit polynom.

Øvingsoppgåve 14.7 Drøft og skisser funksjonen

A (x) = - x + 2 + \frac{1}{x} .

Finn maksimums- og minimumspunkta, og forklar kva som skjer når $x \to 0$ og når $x \to \pm \infty$ .

Øvingsoppgåve 14.8 Drøft og skisser funksjonen

A (x) = - x + 2 - \frac{1}{x} .

Finn maksimums- og minimumspunkta, og forklar kva som skjer når $x \to 0$ og når $x \to \pm \infty$ .

14.3 Kostnadsoptimum †

14.3 Kostnadsoptimum $†$