Veke 11. Funksjonsdrøfting

Eksempeloppgåve 12.7 Drøft og skissér funksjonen

Marker topp- og botnpunkta.

Løysing 12.3 Éin god start er å finna topp- og botnpunkt. Den deriverte er

Topp- og botnpunkta finn me ved å løysa

og formelen gjev

Dette gjev $x=\text{0,549}$ og $x=\text{−1,215}$. Vidare ser me at $f^{\prime }\left(x\right)$ er stor (positiv) for store og små verdiar av $x$. Dvs. at $f\left(x\right)$ aukar fram til $\text{−1,215}$, fell vidare til $\text{0,549}$, og til slutt stig igjen.

Det er òg lett å sjå at $f\left(0\right)=0$, so kurva må gå gjennom origo. Det ser slik ut.

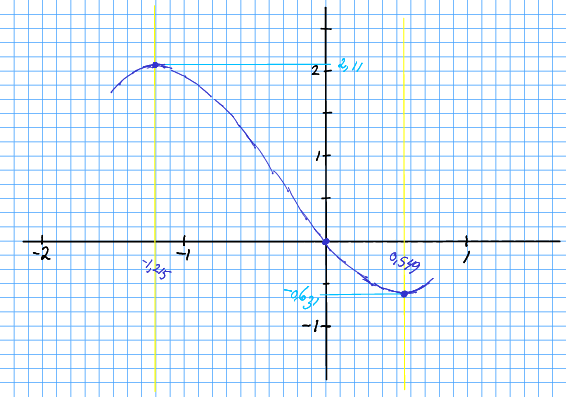
For å finna $y$-verdiane på topp- og botnpunktet, har me sett $x$-verdiane inn i funksjonen, slik

Merk at me ikkje har funne dei to andre nullpunkta nøyaktig. Difor er det berre nullpunktet i origo som me har markert tydleg med ein prikk.

Øvingsoppgåve 12.8 Drøft og skissér funksjonen

Marker topp- og botnpunkta.

Øvingsoppgåve 12.9 Drøft og skissér funksjonen

Marker topp- og botnpunkta.

Eksempeloppgåve 12.10 Drøft og skissér funksjonen

Marker topp- og botnpunkta og skjæringspunkta med aksane.

Løysing 12.4 Me byggjer vidare på skissa frå oppgåve 12.10, der me fann topp- og botnpunkt. No treng me skjæringspunkt med aksane.

Skjæringspunktet med $y$-aksen er enkelt å finna, som funksjonsverdien ved $x=0$. Me skriv

Det er generelt vanskeleg å finna nullpunkta for ein tredjegradsfunksjon, men i dette tilfellet er det enkelt. Der er ikkje noko konstantledd, og dermed kan me dra $x$ utanfor ein parentes:

Når $f\left(x\right)=0$ har med altso anten $x=0$, eller

Andregradslikninga kan me løysa med formel, og me får $x=-2$ eller $x=1$. Totalt har me tre nullpunkt $x=-2,0,1$. Me utvider skissa frå oppgåve 12.10 med ny informasjon.

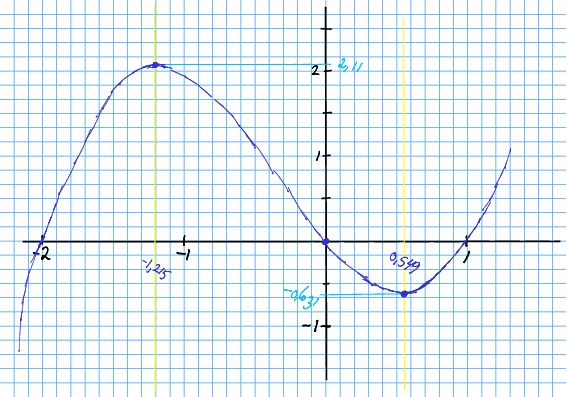
Øvingsoppgåve 12.11 Drøft og skissér funksjonen

Marker topp- og botnpunkta og skjæringspunkta med aksane.

Eksempeloppgåve 12.12 Drøft og skissér funksjonen

Marker topp- og botnpunkta og skjæringspunkta med aksane.

Løysing 12.5 Denne funksjonen har òg $x$ i alle ledda, slik at me kan faktorisera enkelt:

Me har altso eit nullpunkt i $x=0$. Dersom me set parentesen lik null,

og løyser med formel, får me eit negativt tal under rotteiknet, so dette andregradsuttrykket har ikkje noko nullpunkt. Det einaste skjæringspunktet mellom $f\left(x\right)$ og aksane er i origo.

Den deriverte er

Nullpunkta (for den deriverte) er gjeve ved formelen som

Tilsvarande $y$-verdiar er

Me markerer topp- og botnpunkt, samt nullpunktet i origo og teiknar på frihand.

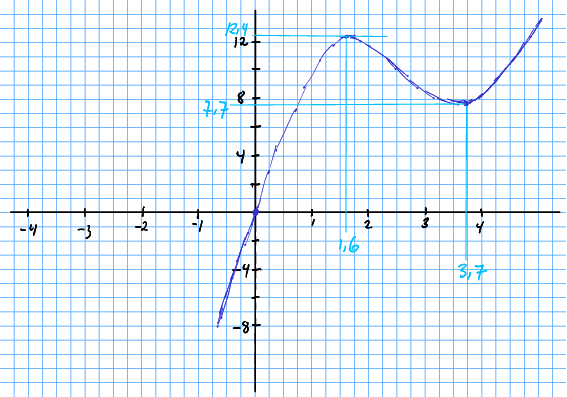
Øvingsoppgåve 12.13 Drøft og skissér funksjonen

Marker topp- og botnpunkta og skjæringspunkta med aksane.

Øvingsoppgåve 12.14 Drøft og skissér funksjonen

Marker topp- og botnpunkta og skjæringspunkta med aksane.

Eksempeloppgåve 12.15 Drøft og skissér funksjonen

Marker topp- og botnpunkta og skjæringspunkta med aksane.

Løysing 12.6 Dette er ein enkel funksjon. Det er lett å sjå at funksjonen er monotont stigande og går gjennom origo. Me får likevel meir informasjon ved å sjå på den deriverte

Den deriverte er 0 akkurat i origo. Kurva åt $f\left(x\right)$ er altso fyrst bratt stigande, flatar ut inn mot origo, men tek so til å stiga igjen, brattare og brattare. Plottet ser slik ut:

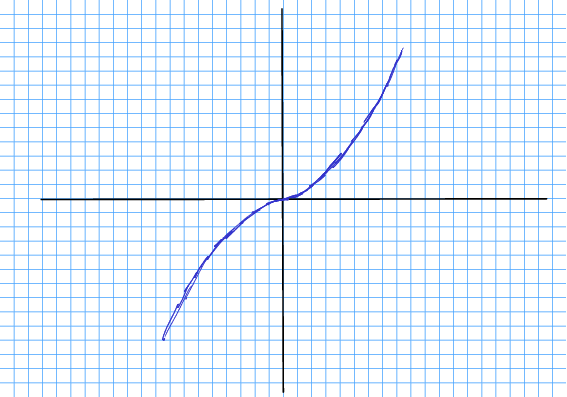
Øvingsoppgåve 12.16 Drøft og skissér funksjonen

Marker topp- og botnpunkta og skjæringspunkta med aksane.

Øvingsoppgåve 12.17 Drøft og skissér funksjonen

Marker topp- og botnpunkta og skjæringspunkta med aksane.