Veke 7. Lineær kostnad og inntekt

Eksempeloppgåve 8.18 Me skal sjå litt meir på bryggeriet frå oppgåve 8.8. Inntektsfunksjonen er $I\left(x\right)=22x$, og kostnadsfunksjonen $K\left(x\right)=10000+7x$.

1.

Finn ein funksjon som fortel kor mykje bryggeriet tener (profitten) når dei produserer og sel $x$ liter øl.

2.

Plott funksjonen og samanlikn han med løysinga frå oppgåve 8.8.

Løysing 8.7 Profitten er differansen mellom inntekt og kostnad, altso

Sidan kostnaden og inntekta er funksjonar av produksjonsvolumet $x$, so må profitten $P\left(x\right)$ òg vera det.

Om me set inn, får me

Grafisk ser det slik ut:

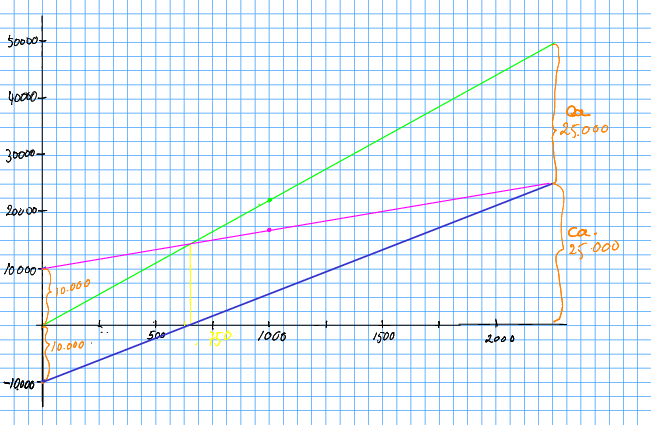
Her har me plotta i same diagram som kostnads- og inntektsfunksjonen, for å kunna samanlikna. Me kan dobbelsjekka at den vertikale avstanden mellom inntekt og kostnad er lik avstanden mellom profitt og null (dvs. $x$-aksen).

Øvingsoppgåve 8.19 Lat oss gå tilbake til sandtaket på Mo i oppgåve 8.9. Inntektsfunksjonen er $I\left(x\right)=600\cdot x$ og kostnadsfunksjonen $K\left(x\right)=\text{100 000}+300x$.

1.

Finn ein funksjon som fortel kor mykje sandtaket tener (profitten) når dei produserer og sel $x$ tonn sand.

2.

Plott funksjonen og samanlikn han med løysinga frå oppgåve 8.9.

Merknad 8.3 Funksjonen som me fann i oppgåva over vert gjerne kalla profittfunksjonen.

Definisjon 8.1 (Lineær funksjon) Alle funksjonane som me har studert so langt har formen $f\left(x\right)=a\cdot x+b$ og når me plottar dei, får me ei rett line. Difor kallar me slike funksjonar lineære.

Definisjon 8.2 (Lineær likning) Når me krev at to funksjonuttrykk skal vera like, f.eks. for å finna balansen mellom kostnad og inntekt, får me ei likning, t.d. 

Når båe sidene i likninga er lineære funksjonar, so seier me at det er ei lineær likning.